The new Punabantu Equation of Exchange*

This is a basic introduction to the new Punabantu Equation of Exchange which supersedes the Irving Fisher Equation of Exchange. The new Punabantu Equation of Exchange demonstrates how Split Velocity is able to increase GDP at constant price by introducing additional “virtual” (split) velocities that allow money to act as a stimulus without inflation due to variances in velocity. This process facilitates the doubling of GDP in one year at constant price by recovering losses being induced in the economy by the defective CFI.

[*Note that these passages are extracted from the book the Greater Poverty and Wealth of Nations (2010) © All Rights reserved, as prescribed by this copyrighted proprietary work and intellectual property.]

Let us use Irving Fisher’s Equation of Exchange as one method to explain how Operating Level Economics (OLE ) accelerated growth works.

The Fisher Equation is as follows:

MV=PT

This is an identity, Where basically:

M- money supply

V-velocity of money

T-total number of transactions made over a period of time

P- value of money

T in the Fisher Equation is not ordinarily linked to output due to the linear economy’s disposition toward zero growth; therefore an increase in transactions ( as it is with an increase in money supply) in a linear economy will be limited by implosion [subtraction in the CFI] and not necessarily lead to an increase in output. However, in a dynamic economy T, which functions on a different growth principle based on split velocity is equated directly to output and is therefore converted to Y or an index value of the physical volume of output in the economy. Therefore, PY in the equation corresponds with GDP.

The Fisher equation is correct as an identity, however, this identity is incomplete as it leaves out one of the most important factors that determine the productive capacity or performance of money in an economy which in turn directly influences the efficiency of production and the general level of output. This factor is the economic operating system in which money (M), Transactions (T) or Output (Y), Velocity (V) and Price (P) function. The operating system is denoted by the letter (R).

The operating system (R) is the number of transactions or allocations of money per cycle. By not including R in the Fisher Equation monetary and fiscal policy as a means of facilitating economic growth and expansion are severely limited.

The world’s economies today function on one transaction (Y) per cycle, that is, R=1. In other words an economy where Y=24 bn has approximately 24 bn transactions per annum occurring at a pace of 1 transaction per cycle, in this case, the cycle is measured over one year. If the economic system where to change to 2 transactions per cycle, that is, R=2, at constant price then output would be YR or 24×2= 48 bn. In other words over the same period of time, that is, 1 year ceteris paribus, the economy could gain the resources to double in size. Instead of one transaction taking place when expenditure takes place the system can make that routine expenditure automatically perform two or more transactions even though the one active expense and choice was made. For example, when a business pays for capital rather than just one transaction taking place the same value is also automatically paid to labour thus performing two transactions in simultaneously. The system (R) determines the rate or pace of productivity though it is not part of the Fisher Equation.

The fact that R=1 makes the ‘operating system’ an invisible property that is not found in the Fisher Equation. It has not been taken into account when using it to formulate policy on money supply in the same way that an equation where the multiplicative factor is constantly 1 will inevitably ignore the factor’s presence. This ‘invisible force’ and the inability to see or account for it is one of reasons why monetary policy has become increasingly unsuccessful in attempts to catalyse growth in modern economies. R can be made visible on the right hand side of the Fisher Equation showing that the system (R) or number of transactions per cycle, determines how many transactions (Y) will take place over a period of time e.g. 1 year:

The system (R) is a module of efficiency. An increase in T is a consequence of a rise in the efficiency of output as a result of a rise in productive efficiency. In the same way that a car travelling at twice the velocity will cover twice the distance over the same period of time the efficiency of R=2 raises the pace of productivity producing twice the volume of output over the same period of time, that is, 1 year.

Money is like a fuel. The more of it the economy burns to do the same work the less efficiently it is functioning, hence inflation is a result. Similarly, an increase in R which is an increase in efficiency has the inverse effect on money supply. It causes output to increase but money supply to shrink (deflation). The less money needed to create output the more efficient the economy. R affects money supply inversely by increasing the efficiency of money which contracts money supply while it raises  the volume of output (Y) inversely. The influence of the factor R appears on the left side as:

Where R=E

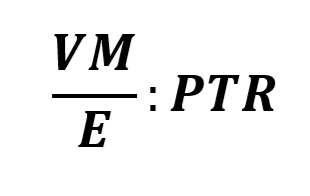
.i.e. VM/E:PTR

The operating system R also affects the velocity of money. When the velocity of money changes it has an interesting effect in that it functions as though there are two economies operating in one space. This occurs as a result of a combined velocity which keeps the velocity of money constant, but working with twice the efficiency. It is based on the system’s dual structure the process which is to be discussed later in this paper.  The factor by which R affects the velocity of money will be denoted as K,  (where K=R).

.i.e. KV(M/E):PTR

However, when the system changes from R=1 to R=2 a money supply deficit is created. There is not enough money in circulation to satisfy the growth in transactions and circulation of goods and services throughout the economy, hence, there arises an inequality seen in the equation above caused by (M/E). When money moves in more than one direction, from one transaction simultaneously performing more than one task, the balance between money supply and productivity must be restored, hence, this adjustment remains within present day monetary policy rules or regulations. The balance is restored by adjusting by S. S is the principle on which split velocity at constant price becomes possible. To do this the fall in money supply (as a result of a change in the system (R) must be increased by R to remain balanced with output. This adjustment at constant price is denoted by S, (where S=R). This last step is significant in that it shows that by changing the system money supply can be turned into a catalyst for growth and development (The stock of money and its behaviour 1-9 provide a more graphic explanation). The final ratio is thus:

The new identity and complete Equation of Exchange, which includes the system in which money functions is as follows:

Where

R – operating system

S – emoney multiplier

E – emoney constrictor

K – virtual velocity

S,E and K are working parts of the operating system dependent on R

In a balanced operating system R=E=K=S

If R=1 in the above equation this reduces it to the original Fisher Equation MV=PT silencing R,E, K and S. This makes the system seem invisible or inconsequential and illusive while it is in fact a useful and yet a missing economic tool. The fact that economies today are linear and function on R=1 entails that MV=PT in a constant operating system. When the system is changed and made to perform dynamically where R>1 or R=2 this creates a sudden money supply deficit or a sudden deflation of 1/R allowing new resources to be created by S (where S=R) simultaneously allocated to capital and households [Split Velocity]. This restores the balance between money supply and output and as a result takes place at constant price in the new system (R=2 or R>1). Inflation does not take place due to the fact that the velocity of money is split allowing it to move in two directions simultaneously. As R is increased on the basis of split velocity as a technological advancement in the use of emoney output or GDP grows by the same rate within the capacity of the technology paradigm. Ceteris paribus by adjusting an economy by R=2 its GDP will double over the same period namely one year supported by the technology paradigm.

R is by no means simply a multiplicative factor, it is part of an operating system. In other words not only does it affect volume it can be manipulated to do so intelligently by changing the process by which allocation takes place thus creating an inverse relationship between money supply and output that can be exploited to catalyse growth and development equally. The equation is systemic meaning it is like a weaving process, the strands or components of the equation may remain the same or be altered, but what is most significant is that the ‘operating system’ or method of weaving changes. The weaving process in this case is the simultaneous allocation of income or finance to households and capital that keeps the dynamic [money moving in more than one direction simultaneously] economy in balance. If the method of allocation raises the number of transactions per cycle this change creates new levels of efficiency, which in turn lead to higher GDP growth rates over the same period of time.

This means that an economy has at its disposal the CFI or “operating system” – (R) as a formidable tool with which to catalyse productivity other than through the four basic factors: money, price, output and velocity alone. R is the system in which these factors operate. A change in R can create a condition in which the four factors can be controlled to obtain desired economic results without negatively affecting an economy.

Making the invisible aspects of the operating system – R hidden in the Equation of Exchange visible is of immense importance to growth and development and opens up new avenues for eliminating poverty, recession and underdevelopment. Here is a more detailed and step by step introduction to the new catalyst and its equation.

The Stock of Money and Its Behaviour

1. The real stock of money (M) or hard cash (notes and coins) in an economy is fixed. It cannot rise or fall unless more or less hard cash is introduced. Money supply on the other hand is relative it can rise and fall despite the amount of notes and coins being constant.

• The way the stock of money behaves however will determine how much money there ‘appears’ to be in an economy. For example, if the velocity of money is two. Though the real stock of money is only 300 bn it will have the impact on the economy of 600 bn (MV). Let us call this the Virtual Stock of Money (Vm).

• The third factor that influences the stock of money  M and the virtual stock of money Vm is the system in which it operates. The system is determined by the number of transactions per cycle. A cycle is the duration during which a single unit of money performs a single task. If the total stock of available financial resources or a unit of money can only be allocated to one task at a time e.g. producing or consuming, as is the case with the world’s economies today, then it is linear. If money per unit of currency were allowed to move from being linear (one transaction at a time) , that is, either producing or consuming to doing both at the same time then the number of transactions it is capable of performing per cycle would increase by 2 (split velocity) and the system would no longer be linear but dynamic. When (R=2) the Virtual stock of money falls by half or by the value of R.

• What happens in 3 as a result of a change in the economic system is very important due to the fact that it means an  inverse effect on money supply and GDP takes place. Altering the economic operating system* entails changing it  from 1 transaction per cycle to two transactions per cycle. This increase in efficiency causes the supply of goods and services to rise while money supply falls. This inverse relationship is important. By introducing it between VM and PT it becomes possible to manipulate the economy using the economic operating system to restore the balance. The restoration facilitates a system that enables growth in output. It is something that it is practically impossible to do in a linear economy.

* Note that the operating system or economic operating system (eos) refers to the circular flow of income (CFI) and can be used interchangeably.

• What happens in 4 is an important development as it means that by altering the CFI or economic operating system (R) governments can shrink the virtual size of money supply and allow it to be optimised , that is, on the dynamic principle [dynamic is two allocations of finance per transaction e.g. to households and capital, rather than just one], which uses this to create new resources for capital (industry) and households. The impact of this discovery is as important to growth and development as the impact of credit creation on investment and opens the door to a whole new net-cash catalyst industry that complements credit creation managed by the banking industry. The catalyst at R=2 is capable of generating new financial resources for eliminating poverty, it is capable of doubling output, doubling productivity, it increases financing available for public works and increases the impact of AID provided by domestic and international agencies. It is capable of putting nations back on track to recovery, economic growth, economic development and a higher general standard of living without some of the harmful consequences of interest rate cuts or utilisation of government reserves to finance public expenditure. It also significantly increases the resources available to banks for credit creation and to domestic and international AID/development agencies for programmes and projects. Furthermore, it significantly increases the dexterity with which central and federal banks can regulate an economy in order to protect it from recession and shocks.

• When an economic system advances e.g. from being linear [where finance moves in one direction per transaction .i.e. Split Velocity] to being dynamic [finance moves in more than one direction per transaction], the efficiency of money (Em) rises (due to the Virtual stock of money falling thus enabling dynamic allocation). At a constant velocity of money  the work done by a unit of money increases and when this happens the Virtual stock of money appears to shrink. For example, the real stock of money may be 300 bn. This money works at a velocity of 2. The economy behaves as though there is 600 bn circulating through it due to the fact that this money circulates through the economy twice per annum. It therefore sustains a GDP of 600 bn where the general price level is 25 and output is 24 bn.

• If the economic [operating] system (CFI) changes from being linear to being dynamic , that is, from one transaction per cycle (R=1) to two transactions per cycle (R=2) the virtual stock of money will appear to shrink by half. This is due to money being made more efficient by performing two tasks simultaneously rather than one. This is as a result of a change in the economic system. (To illustrate this, it is like a mule (money) pulling a single cart (number of transactions) over a distance in a pace of time (velocity) required by the market. There is only one mule transporting goods and services (facilitating productivity). The mule is pulling its maximum load. No more transactions can be added to this system otherwise it slows the mule down (deflation) making it too slow to deliver its goods required by the market on time. Neither can another mule (additional money) be added to the same load to speed things up as the cart would arrive at the market before all its goods were ready for sale (inflation). By increasing the work done by money (R=2 transactions per cycle) another cart of equal size and load is harnessed to the mule. The load of productivity becomes too heavy for one mule to pull. This slows it down (making the stock of money shrink (virtual deflation). This alteration makes it possible to introduce another mule (new financial resources created by the operating system) to help tow the two carts at constant price. Now there are two mules pulling two equal loads (split velocity) facilitating twice the level of output (GDP) at the pace required by the market to get the goods there on time). The additional mule harnessed to a dynamic operating system (CFI) creates new resources 300 bn to 600 bn. When this happens the Virtual velocity of money (K) pushes this value up to 1.2 trillion at constant price. This is necessary since the velocity of money flowing in either direction (toward capital and toward households) remains constant at 2. The split in allocation (split velocity) creates two economies functioning simultaneously, namely the capital economy working at a velocity of 2 and the consumer economy working at a velocity of 2. This creates a combined virtual velocity of 4 per annum, however, money is moving only at a velocity of 2 per annum in its respective capital and consumer economies which though fully integrated are separately fueled (by money).  In consideration of the older Fisher Equation even if ‘transactions’ remains constant since money appears to be operating in two economies. This split velocity is extremely important as it keeps the general price level at 25 while output increases from 24 bn to 48 bn. It keeps the velocity of money at 2 (in each economy) allowing the stock of money to grow from 300 bn to 600 bn. This will be reflected by the value K in the equation. A change in the economic [operating] system (CFI) from R=1 (linear) to R=2 (dynamic) will cause the efficiency of output to double from 600 bn GDP per annum to 1.2 trillion GDP over the same period of time at constant price generally allowing a doubling of output in an economy per year.

• The addition of 300 bn to the real stock of money restores the deficit created by advancing the financial system from R=1 to R=2 (M/E) and this restoration (S) at a constant velocity of money of 2 doubles the output from 24 bn to 48 bn raising GDP from 600 bn to 1.2 trillion over the same period of time. This situation keeps the economy in balance with 1.2 trillion VM servicing 1.2 trillion GDP. The dynamic economy or dynamic operating system is in this case twice as efficient, twice as productive, twice as able to provide and twice as stable as the linear economy. When the system remains linear, that is, R=1, as the world’s economies are today, then GDP growth rates will be encouraged to balance at zero. In other words linear economies are designed to remain stagnant [this stagnance or lack of growth is why a linear economy is referred to as a “zero growth economy”] To grow they must rely on cost plus pricing, more on which is discussed later. This is why they annually produce such poor levels of output that economies and economists have become accustomed to. To overcome stagnation industry and households have to ‘overwork’ themselves or use surplus efficiency to survive. The result is a salvaged annual GDP that often resides between a paltry 0-10% per annum. When GDP accelerates to levels as high as 65% as observed in some oil producing countries as a result of oil, the economy is not inherently designed to distribute wealth equally between capital households thus leading to growth without development, that is, growth while poverty levels remain high. This causes adverse or artificial scarcity from which present day poverty and its plethora of socio-economic problems arise. The switch from a linear to a dynamic operating system at (R=2) doubles the level of financing in an economy, ceteris paribus, allowing a doubling of GDP over the same period of time. It means that the US economy has the potential to grow from US$12.5 trillion in GDP (IMF 2005) to US$25 trillion in one year ceteris paribus; the US government may not need all these resources and may not need the economy to grow this quickly and could instead capture the percentage of these resources it felt was required for its population and needs. It means that the South African government has the potential to make the South African economy grow from US$240bn (IMF 2005) to US$480 bn a year. It means that the EU could make its economy grow from US$13.5 trillion (IMF 2005) to US$27  trillion in a year.  It means that the Zambian government cold make the Zambian economy grow from US$7.3 bn to (IMF 2005) to US$14.6 bn in a year. Since this Operating Level Economics (OLE) .i.e. circular flow of Income economic method acts as a catalyst this growth is natural allowing the economy to expand the same way it would if left to itself except in a much shorter duration of time. There is no hocus-pocus involved. Nations are in this case no longer limited by the linear operating system’s implosionary limitations [limitations caused by subtraction] and losses that lead to very low annual growth rates. They can grow much faster and at a rate that they deem fitting. Any well managed linear economy can increase GDP in this way without breaking a sweat due to the fact that it is already operating at level required to do so only implosion [subtraction in the CFI] dissipates the potential output it should naturally have access to. Dynamic allocation naturalises or balances productivity and output that implosion [subtraction in the CFI] in a linear economy has kept persistently unequal. When economies become dynamic [more than one allocation of finance per transaction] they acquire a rate of growth that they should have been exposed to all along. Artificial scarcity and the problems it creates are no longer a limit to what governments can achieve for betterment of their people. If the US government felt that it needed to grow by only 36% more in a year to create enough productivity within the US economy to wipe out industrial stagnance, squalor in inner cities, poverty, unemployment and create a general standard of living in line with government policy then the US Federal Reserve Bank would regulate the economy to R=1.36 rather than the full R=2.  In other words it would capture only 36% of its total potential to grow in that year as allowing growth by the remaining 64% may be considered too excessive or extravagant for the existing population. A balance is thus found that avoids the problems caused by adverse scarcity and adverse surpluses. For African nations trying to find sustainable resources for projects like NEPAD transforming from a linear to dynamic operating system provides an alternative route to sustainable development and development financing. In this case governments are in a better position due to the fact that they control the availability of resources rather than being controlled for the worse by artificial scarcity, which is averse to socio-economic development.

• Finally, the new equation for money moves on from the monetarist Fisher Equation:

MV=PT

To the new Punabantu Equation of Exchange:

Where R=E=K=S R is the economic [operating] system in which Money (M), Velocity of money (V), Price (P) and Output (Y) function. The values R=E=K=S in the equation [above] remain equal. Money Supply M has to be multiplied by whatever it is made to virtually shrink by 1/E. In this case money supply is made to shrink by the economic system R=2 therefore the real stock of money has to be increased by the proportionate value of R which is represented as S otherwise there will be a deficit in the real stock of money M. However, this increase takes place on an alternate velocity thus causing no change in the general price level, but rather the alternate side effect, that is, an increase in growth. To prove this S can be cancelled out by R in the equation (also using a concept of mechanical efficiency) due to the fact that though money supply is doubled (from 300 bn to 600 bn) to facilitate productivity in the restructured economic [operating] system its virtual value remains 300 bn due to the fact that it does not change along the same velocity. This is an important benefit of dynamic allocation. M is a real quantity while R, its common denominator, is a virtual one determined by the mechanical level of efficiency present in the economy (R=2). Modern economies are linear systems (R=1). Any attempts to increase money supply will lead to an increase in the general price level (inflation). The dynamic economy therefore offers new hope to ailing economies as a catalyst with which to boost productivity and consumption equally without using external resources. It is also a new tool by which to increase and accelerate annual GDP growth rates and bring an end to poverty, unemployment, stagnation and economic instability.

The equation satisfies both Monetarist and Keynesian schools of thought in that it creates new resources in S to catalyze productivity and yet the increase has no impact on inflation due to the fact that it is cancelled out by 1/E. K,V,S and E become constants. K is representative of the fact that money flowing to consumers (households) and capital (raw materials, equipment, repayment of loans etc.) does so at the same velocity (V), however, they take place simultaneously creating a Virtual Velocity (Vv) of 4 (Vv=KV=2×2) seen by a dual economy delivering financing output at the same velocity, but at double the volume (two carts: split velocity). The change in R from R=1 to R=2 causes money supply to shrink (M/E) making it necessary to restore its value by S; (MS/E) This works fine since it allows the stock of money to double and yet appear to remain the same (adding another mule). Doubling goes hand in hand with it being allocated equally and simultaneously to capital and households creating the R=2 economy (doubling the load by adding an additional cart) in which growth and development rise equally rather than one above or before the other. The increase in productive efficiency allows the stock of goods to increase by YR rather than just Y over the same period of time (1 year).

In terms of the efficiency of money an economy shrinks by M/E and must be restored to MS by S were as the inverse occurs and output grows by YR where R=S.

The economic system R (the number of transactions per cycle) is  a non-obtrusive catalyst. It acts inversely on money and output by increasing the rate of productivity that lowers money supply allowing it to be expanded while making it possible for producers to expand output. This allows economic expansion (growth + development) to take place rather than one at the expense of the other. This is a significant improvement in economic management.

MONETARY THEORY & ACCELERATED GROWTH IN A NUT SHELL

OLE theory states that, ceteris paribus, every economy at any point in time contains within its economic operating system the latent financial resources with which to double its GDP in one year at constant price. Therefore, economies are capable of geometric gains in growth as opposed to the linear gains in GDP observed today.

The Fisher Equation and Punabantu Equation

The Fisher Equation is as follows:

MV=PT

This is an identity, where basically:
M- money supply

V-velocity of money

T-total number of transactions made over a period of time e.g. 1 year

P- general price level

T in the Fisher Equation is not ordinarily linked to output due to the linear economy’s disposition toward zero growth; therefore, an increase in transactions as it is with an increase in money supply in a linear economy will be limited by implosion [subtraction in the CFI] and not necessarily lead to an increase in output. However, in a dynamic economy T, which functions on a different growth principle based on split velocity  is equated directly to output and is therefore converted to Y or an index value of the physical volume of output in the economy. Therefore, PY in the equation as will be seen to correspond with GDP.

Moving from the Fisher Equation to the Punabantu Equation: The new identity and complete Equation of Exchange, which includes the system in which money functions is as follows:

Where

R – operating system

S – emoney multiplier

E – emoney constrictor

K – virtual velocity

Y – output of goods and services

S,E and K are working parts of the operating system dependent on R where R=E=K=S

If R=1 in the above equation this reduces it to the original Fisher Equation MV=PT silencing R,E, K and S. This makes the operating system seem invisible or inconsequential and illusive while it is in fact a useful and a yet missing economic tool in growth and development. The fact that economies today are linear and function on R=1 entails that MV=PT in a linear operating system and T rather than Y should be used in the equation.

The annual rate at which output grows (GDP) is determined by the operating system and the technology paradigm (organisation of human skills and capital to create a desired level of productivity.)

Where M=300, Velocity=2, P=US$25, Y=24 bn

If the economy is linear as it is with economies today then R=1 therefore growth does not benefit from the operating system’s accelerant . For example: .

PYR=25x24x1= US$600bn, Therefore, GDP is US$600 bn for the year

If the operating system is used to double growth over 1 year, that is, R=2

PYR= 25x24x2 = US$ 1,200 bn over the same period; therefore GDP has the potential to double to US$1,200 over the same period.

This accelerated growth takes place at constant price:

.i.e. P=KV(MS/E)/YR= 1,200/24×2=US$25

Accelerated growth is geometric allowing doubling to take place each consecutive year; significantly shortening the pace at which development occurs.

Hence, using the new Punabantu Equation of Exchange, as demonstrated in the equation above by the doubling of GDP from $600bn to $1,200 bn in one year, where the price level remains constant at $25, it is verified mathematically that an economy can finance the doubling of its GDP in one year at constant price. The new equation of exchange confers sovereign economic status on an economy as it allows a domestic currency to be minted and introduced into circulation where instead of generating inflation it acts as a stimulus for growth and development. It allows governments to grow their economies until productivity is on par with the needs of a given population.

[Note that doubling time (the rate of economic growth each year) does not have to be fully applied. It can be applied by percentage anywhere between 0% – 100%. The pace at which an economy can grow is determined by its technology paradigm.]